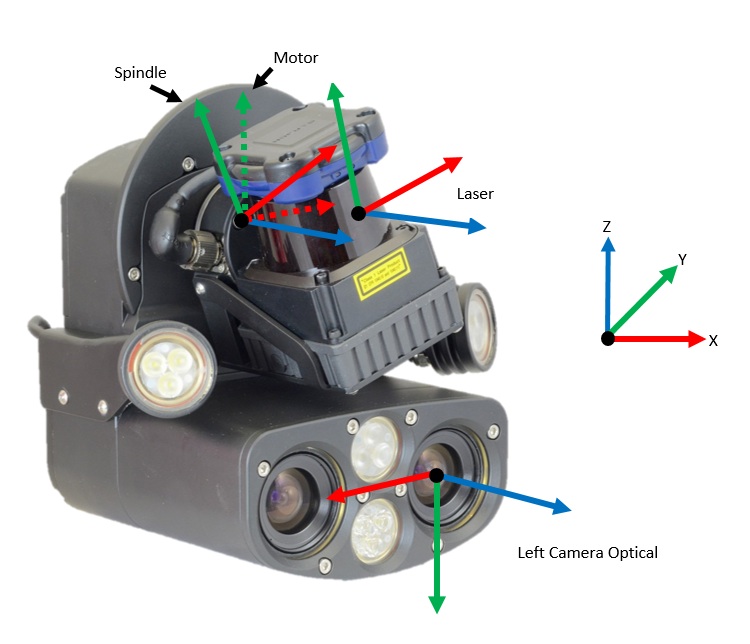
7. Transforms
The MultiSense SL unit stores a unique calibration to transform laser range data into the left camera optical frame. This calibration is comprised of two static transforms; one from the motor frame to the left camera frame, the other from the laser frame to the spindle frame. There is an additional transform between the spindle frame and the motor frame which accounts for the rotation of the laser spindle.
The MultiSense ROS driver automatically generates a transform tree based on these three transforms. Additionally both the ROS driver and the underlying API offer mechanisms to perform custom transformations of laser data. The following sections detail this transform tree and provide a basic example of how to perform this transformation.
7.1. Overview
The MultiSense SL has three primary transforms between the four coordinate frames which are used to transform laser range data into the left camera optical frame.
The first transform is a static transform between the fixed motor frame and the left camera frame which is described by the homogeneous transform matrix HCM. In the ROS driver this transform is referred to as cameraToSpindleFixed.
The second transform is between the spindle frame and the fixed motor frame which is described by the homogeneous transform matrix HMS. This transform accounts for the spindle frame’s rotation about the z-axis of the fixed motor frame as the laser spins.
The final transform is static between the laser frame and the spindle frame which is described by the homogeneous transform matrix HSL. In the ROS driver HSL is referred to as laserToSpindle. By multiplying these homogeneous transform matrices together a laser range point in Cartesian space can be transformed into the left camera frame.
dc = HCM * HMS * HSL * dL
Where dL is a 4x1 matrix representing a single laser point in the x-z plane of the laser’s local frame and dc is a 4x1 matrix representing a single laser point in the left camera’s optical frame.
7.2. Tree
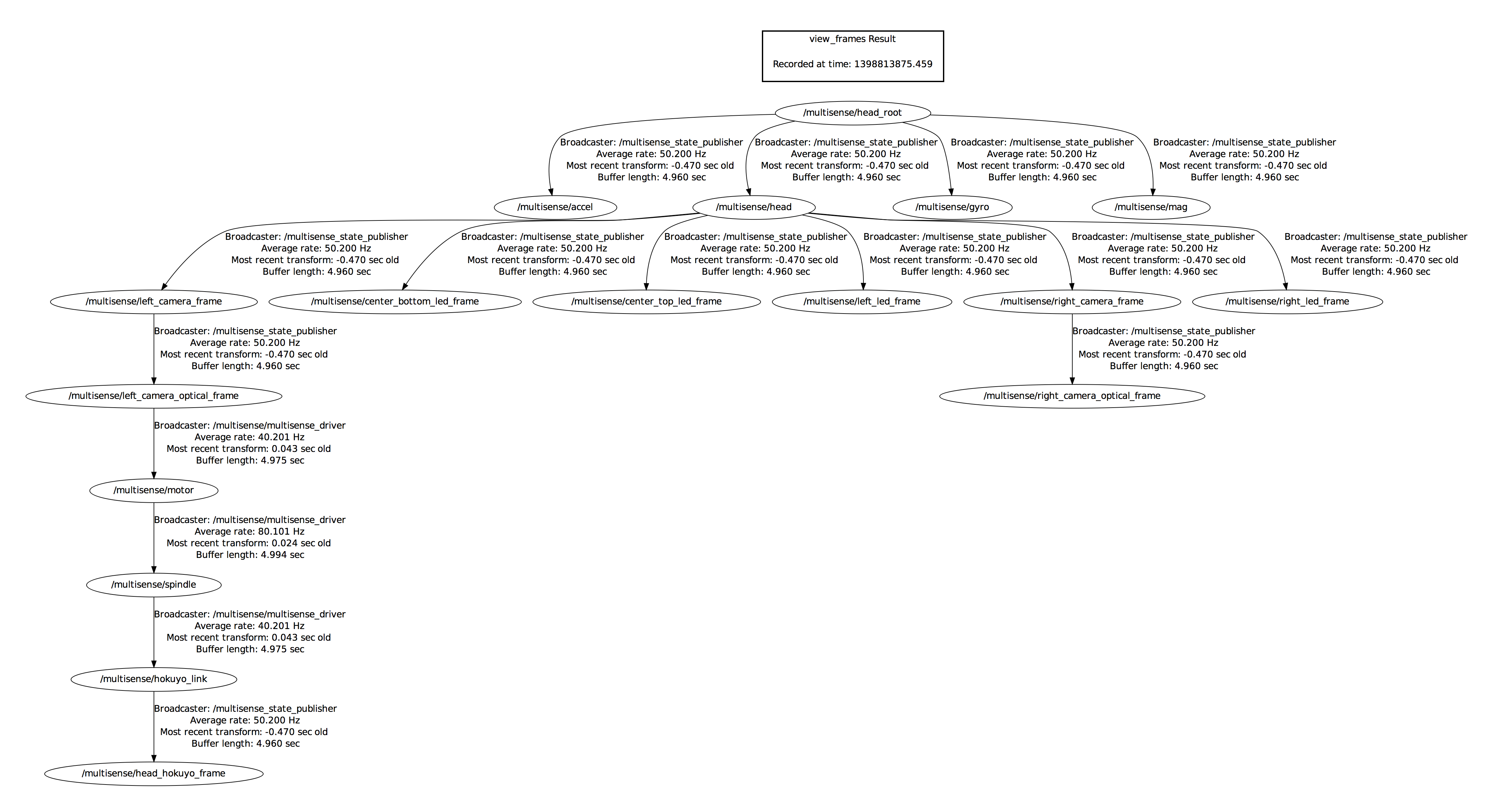
The MultiSense ROS driver uses the robot_state_publisher ROS package to create the initial transform tree using the URDF file in the multisense_description package. In addition, the robot_state_publisher and /multisense/joint_states messages are used to manage the transform between the motor and laser spindle corresponding to HMS.
| Transform | From Frame | To Frame |
|---|---|---|
HCM |
|
|
HMS |
|
|
HSL |
|
|
A final static transformation between /multisense/hokuyo_link and /multisense/head_hokuyo_frame is required to properly display the /multisense/lidar_scan topic in RViz.
The full ROS transform tree is shown below.
7.3. Interface
The MultiSense ROS driver offers three primary mechanisms to process and view laser data: the /multisense/lidar_scan, /multisense/lidar_points2, and /multisense/calibration/raw_lidar_data topics. In addition to laser data, the driver presents the raw calibration matrices on the /multisense/calibration/raw_lidar_cal topic.
7.3.1. Scan Topic
The /multisense/lidar_scan topic is a sensor_msgs/LaserScan message containing the raw laser range and intensity data in polar coordinates along with information used to interpolate the Cartesian position of each range reading.
The transformation of the laser data into the /multisense/left_camera_optical_frame is managed by the transform tree constructed by the robot_state_publisher and the per-scan published full HCM and HSL transforms managed by the ROS driver.
When the laser is spinning the motion between individual range returns is compensated by ROS internally using SLERP. This interpolation can also be used to account for external motions of the head; assuming the MultiSense-SL’s transform tree is a child of the frame in which the motion is occurring.
7.3.2. Points2 Topic
The /multisense/lidar_points2 topic is a sensor_msgs/PointCloud2 message which contains laser data transformed into the /multisense/left_camera_optical_frame.
Each laser scan is published as an individual point cloud.
When transforming the laser data into Cartesian space both the scan angle and the spindle angle are linearly interpolated.
This transformation is done without knowledge of external forces that may be acting on the sensor.
7.3.3. Raw Topic
The /multisense/calibration/raw_lidar_data and /multisense/calibration/raw_lidar_cal are a custom message types which contain all the information necessary to manually transform the laser data into the /multisense/left_camera_optical_frame.
The /multisense/calibration/raw_lidar_data topic contains the raw laser data as well as information about the angle of the spindle frame at the start and end of the laser scan.
The /multisense/calibration/raw_lidar_cal topic contains the two static calibration transforms 𝐻𝑀𝐶 and 𝐻𝐿𝑆 flattened to 16 element arrays in row-major order. Using these two topics the laser data can be manually transformed using a custom interpolation scheme external of the MultiSense SL ROS driver.
7.4. External Example
The following excerpts of code use ROS’s TF and Angles packages to transform laser data into the /left_camera_optical_frame.
The example consists of two subscribers; one to the /laser/calibration/raw_lidar_data topic and the other to the /laser/calibration/raw_lidar_cal topic.
// Create two TF transforms for the Camera to Spindle calibration and the Laser
// to Spindle calibration
void rawLaserCalCallback(const multisense_ros::RawLidarCal::ConstPtr& msg)
{
//Get Transform Matrices from flattened 16 element Homogenous arrays in
// row-major order
_laserToSpindle = makeTransform(msg->laserToSpindle);
_motorToCamera = makeTransform(msg->cameraToSpindleFixed);
}
template <typename T> tf::Transform makeTransform(T data)
{
// Manually create the rotation matrix
tf::Matrix3x3 rot = tf::Matrix3x3(data[0],
data[1],
data[2],
data[4],
data[5],
data[6],
data[8],
data[9],
data[10]);
// Maually create the translation vector
tf::Vector3 trans = tf::Vector3(data[3], data[7], data[11]);
return tf::Transform(rot, trans);
}The above code constructs two http://docs.ros.org/api/tf/html/c/classtf_1_1Transform.html[tf::Transfrom] objects, __laserToSpindle_ and __motorToCamera++, from a single _/multisense/calibration/raw_lidar_cal message. These Frames correspond to HSL and HCM respectively.
// Transforms Laser Data using onboard calibration
void rawLaserDataCallback(const multisense_ros::RawLidarData::ConstPtr& msg)
{
// For Visualization
makePointCloudHeader(msg->distance.size());
_point_cloud.header.stamp = msg->time_start;
uint8_t *cloudP = reinterpret_cast<uint8_t*>(&_point_cloud.data[0]);
const uint32_t pointSize = 3 * sizeof(float);
// Scan angle range of the laser
const double fullScanAngle = 270 * M_PI / 180.;
// Laser start at -135 degrees spinning counterclockwise
const double startScanAngle = -fullScanAngle / 2.;
// Get the spindle angles for this scan. angle_start and angle_end are in micro-radians
// Use ros package angles to normalize them to -PI to +PI
const double spindleAngleStart = angles::normalize_angle(1e-6 * static_cast<double>(msg->angle_start));
const double spindleAngleEnd = angles::normalize_angle(1e-6 * static_cast<double>(msg->angle_end));
const double spindleAngleRange = angles::normalize_angle(spindleAngleEnd - spindleAngleStart);
// Loop over all the range data
for ( unsigned int i = 0; i < msg->distance.size(); i++, cloudP += _point_cloud.point_step){
// Percent through the scan. Used for linear interpolation
const double percent = static_cast<double>(i) / static_cast<double>(msg->distance.size() -1);
// Linearly interpolate the laser scan angle from -135 to 135
const double mirrorAngle = startScanAngle + (percent * fullScanAngle);
// Linearly interpolate the spindle angle
const double spindleAngle = spindleAngleStart + (percent * spindleAngleRange);
// Generate the Homogeneous Transform for the Motor to Spindle Transform
const double cosSpindle = std::cos(spindleAngle);
const double sinSpindle = std::sin(spindleAngle);
_spindleToMotor = tf::Transform(tf::Matrix3x3(cosSpindle, -sinSpindle, 0,
sinSpindle, cosSpindle, 0,
0 , 0, 1),
tf::Vector3(0, 0, 0) );
// Convert range point to meters and project into the X-Z laser plane
const double rangeMeters = static_cast<double>(1e-3 * msg->distance[i]);
const tf::Vector3 rangePoint = tf::Vector3(rangeMeters * std::sin(mirrorAngle),
0,
rangeMeters * std::cos(mirrorAngle));
// Transform point into the left camera frame
const tf::Vector3 pointInCamera = _motorToCamera
* (_spindleToMotor
* (_laserToSpindle * rangePoint));
// Copy data to point cloud structure
const float xyz[3] = {static_cast<float>(pointInCamera.getX()),
static_cast<float>(pointInCamera.getY()),
static_cast<float>(pointInCamera.getZ())};
memcpy(cloudP, &(xyz[0]), pointSize);
memcpy((cloudP + pointSize), &(msg->intensity[i]), sizeof(uint32_t));
}
_point_pub.publish(_point_cloud);
}
void makePointCloudHeader(const unsigned int pointCount)
{
const uint32_t cloud_step = 16;
_point_cloud.data.resize(cloud_step * pointCount);
_point_cloud.is_bigendian = (htonl(1) == 1);
_point_cloud.is_dense = true;
_point_cloud.point_step = cloud_step;
_point_cloud.height = 1;
_point_cloud.header.frame_id = "/multisense/left_camera_optical_frame";
_point_cloud.fields.resize(4);
_point_cloud.fields[0].name = "x";
_point_cloud.fields[0].offset = 0;
_point_cloud.fields[0].count = 1;
_point_cloud.fields[0].datatype = sensor_msgs::PointField::FLOAT32;
_point_cloud.fields[1].name = "y";
_point_cloud.fields[1].offset = 4;
_point_cloud.fields[1].count = 1;
_point_cloud.fields[1].datatype = sensor_msgs::PointField::FLOAT32;
_point_cloud.fields[2].name = "z";
_point_cloud.fields[2].offset = 8;
_point_cloud.fields[2].count = 1;
_point_cloud.fields[2].datatype = sensor_msgs::PointField::FLOAT32;
_point_cloud.fields[3].name = "intensity";
_point_cloud.fields[3].offset = 12;
_point_cloud.fields[3].count = 1;
_point_cloud.fields[3].datatype = sensor_msgs::PointField::UINT32;
_point_cloud.row_step = pointCount;
_point_cloud.width = pointCount;
}The above code generates a tf::Vector3 object pointInCamera which contains the x, y, and z coordinates of a single laser range point transformed into the /multisense/left_camera_optical_frame. The code linearly interpolates the laser scan angle as it spins counterclockwise from -135 degrees to 135 degrees. The angle of the spindle, originally published in micro-radians, is also linearly interpolated to compensate for motion due to the rotation of the spindle.